biharmdiag

Biharmonic coefficients of a diagonal band by sublock

Syntax
Description
Example
Input Arguments
Returns:
See Also

Syntax

[d0,d1,dc,dM1,dM0] = biharmdiag(BCs,h,D,nu,dia)

Description

[d0,d1,dc,dM1,dM0] = biharmdiag(BCs,h,D,nu,dia) returns a 5-by-5 matrix of biharmonic coefficients where columns represents the diagonal blocks d0,d1,dc,dM1,dM0 for the diagonal given by dia

Example

%% second offset diagonal '-2Ny'
a0 = ones(Ny+1,1) ;
a1 = ones(Ny,1) ;
a2 = ones(Ny-1,1) ;

[~,~,dc,dM1,dM] = biharmdiag(BCs, h, D, nu,'-2ny');

dm2Ny0 = dc(3)*a0;
dm2Ny0([1,2,Ny,Ny+1]) = [dc(1),dc(2),dc(end-1),dc(end)];

dm2Ny1 = dM1(3)*a0;
dm2Ny1([1,2,Ny,Ny+1]) = [dM1(1),dM1(2),dM1(end-1),dM1(end)];

dm2Ny2 = dM(3)*a0;
dm2Ny2([1,2,Ny,Ny+1]) = [dM(1),dM(2),dM(end-1),dM(end)];

Dm2Ny = [repmat(dm2Ny0,Nx-3,1);dm2Ny1;dm2Ny2];

Input Arguments

BCs : 4-by-2 matrix of elastic boundary constants, in the order y0, x0, yL, xL
h : Grid spacing
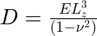
D : Stiffness constant $D = \frac{E L_z^3}{(1-\nu^2)}$
nu : Poisson's ratio
dia : String representing the offset of the diagonal Index of coefficient. Valid diagonals are ['-2ny','-ny-1', '-ny', '-ny+1', '-2', '-1', '0', '1', '2', 'ny-1', 'ny', 'ny+1','2ny']

Returns:

Outer coeffients diagonal blocks for the given dia will be filled with NaN values if they do not apply

d0 : diagonal coefficient for index 0
d1 : diagonal coefficient for index 1
dc : diagonal coefficient for central points
dM1 : diagonal coefficient for Ny - 1
dM0 : diagonal coefficient for Ny